Die Schickard Rechenmaschine von 1623
Die erste mechanische Rechenmaschine, die alle vier Grundrechenarten und sogar das Wurzelziehen unterstützte,
wurde 1623 vom Tübinger Professor Wilhelm Schickard (1592-1635) erfunden
und von seinem Mechaniker Johann Pfister gebaut.
Die Maschine bestand aus drei Bauteilen: einem Addierwerk, einem Multiplizierwerk sowie einem Zwischenspeicher für eine sechsstellige Dezimalzahl.
Das Addierwerk beherrschte den automatischen Zehnerübertrag bei Addition und Subtraktion.
Das Multiplizierwerk basierte auf den Napierschen Rechenstäbchen von 1617.
Ein zweites Exemplar sollte 1624 für Schickards Freund Johannes Kepler gebaut werden, wurde aber noch vor der Fertigstellung durch einen Brand zerstört.
Nachdem Wilhelm Schickard mitten im Dreißigjährigen Krieg nach der Besetzung Württembergs durch kaiserliche Truppen mitsamt seiner Familie an der Pest starb,
gerieten er und seine Erfindung in Vergessenheit, sodass lange
Blaise Pascal als Erfinder der ersten Rechenmaschine galt.
In den 1930er Jahren wurden im Nachlass Johannes Keplers zwei Briefe gefunden, die Schickard an seinen Freund Kepler geschrieben hatte.
In diesen Briefen beschrieb Schickard seine Rechenmaschine und ihre Bauteile.
Es wurden auch zwei Skizzen der Rechenmaschine
sowie Konstruktionsanweisungen Schickards an seinen Mechaniker Johann Pfister gefunden.
Anhand dieser Unterlagen gelang es dem Tübinger Professor
Bruno von Freytag-Löringhoff
in dreijähriger Arbeit von 1957 bis 1960 die Maschine zu rekonstruieren
und einen funktionsfähigen Nachbau anzufertigen.
Bauteile
- Multiplizierwerk
- Addierwerk
- Zwischenspeicher
Multiplizierwerk
Das Multiplizierwerk besteht aus sechs drehbaren Zylindern, die jeweils zehn Seiten haben und für die Ziffern von null bis neun die errechneten Ergebnisse des kleinen Einmaleins enthalten. Durch Schieberegister kann jeweils die Reihe des aktuellen Multiplikators geöffnet werden, die gerade für die Multiplikation oder Division benötigt wird. Die Reihen der nicht benötigten Multiplikatoren bleiben dagegen verborgen und stören dadurch beim Ablesen nicht.
Das Multiplizierwerk und die Multiplikation werden im Video "Multiplikation mit der Schickard-Rechenmaschine" erläutert. Dort wird auch die Multiplikation mit den von John Napier erfundenen Rechenstäbchen erläutert, da diese die Grundlage für das Multiplizierwerk der Schickard-Rechenmaschine darstellen.
Die Division wird als umgekehrte Multiplikation berechnet. Dies wird im Video "Division mit der Schickard-Rechenmaschine" gezeigt.
Addierwerk
Das Addierwerk ist das Herzstück der Schickard-Rechenmaschine, da es für alle vier Grundrechenarten benötigt wird und bei weitem der mechanisch aufwendigste Teil der Maschine ist.
Es besteht aus folgenden Teilen:
- sechs Zahlenwalzen zur Darstellung jeweils einer Dezimalstelle, jeweils mit den Ziffern null bis neun
- sechs Sichtfenster an der Oberseite des Addierwerks zum Ablesen der eingestellten Dezimalzahl (es ist jeweils nur die aktuelle Ziffer der darunter liegenden Zahlenwalze sichtbar)
- sechs Einstellräder oder Wählscheiben an der Vorderseite des Addierwerks, zum Einstellen der gewünschten Zahl
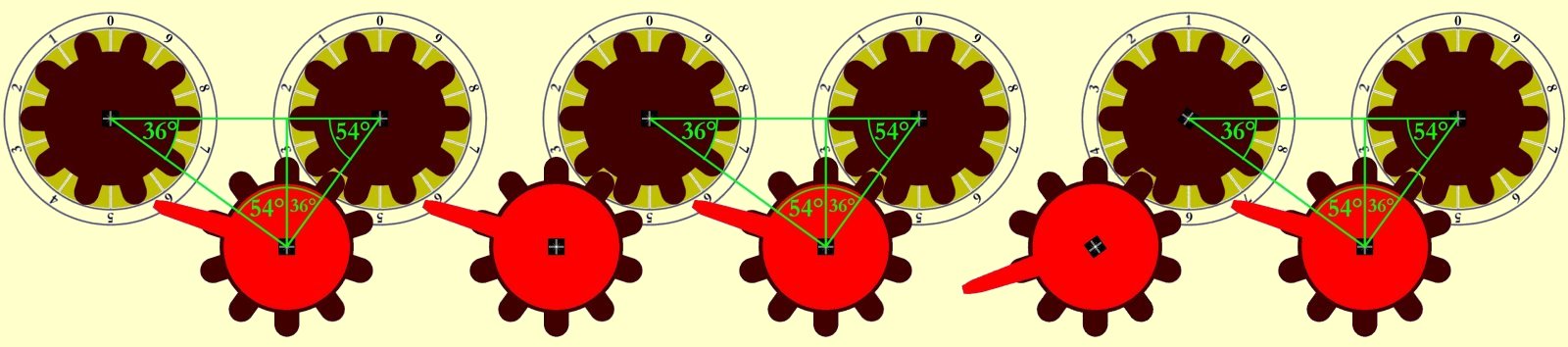
- 11 Zahnräder mit jeweils zehn Zähnen (sechs zur Darstellung der Dezimalstellen, sowie fünf zusätzliche Räder zur Gleichrichtung der Drehbewegung der sechs Haupt-Zahnräder)
- fünf Einzahn-Zahnräder, die den automatischen Zehnerübertrag in die nächst höhere Stelle bewerkstelligen
- optional eine Rasterung, die das Blockieren oder Überdrehen der Zahnräder verhindert.
Damit das Addierwerk möglichst störungsfrei funktioniert, ist es ganz wichtig, dass die Zahnräder in genau definierten Winkeln zueinander angeordnet sind. Der Winkel 36° ergibt sich durch 360° / 10. Der Winkel, den jeweils zwei Haupträder mit einem Hilfsrad bilden, soll möglichst genau 90° sein. Der dritte Winkel von 54° ergibt sich dann automatisch.
Der Aufbau und die Funktionsweise des Addierwerks werden im Video "Addition und Subtraktion mit der Schickard-Rechenmaschine" erläutert.
Zwischenspeicher
Der Zwischenspeicher dient dazu, eine bis zu sechsstellige Dezimalzahl zu speichern. Dies wird in den Berechnungen aller vier Grundrechenarten benötigt.
Der Zwischenspeicher ist sehr einfach konstruiert. Er besteht aus sechs drehbaren Zahlenscheiben, die mit den Ziffern von null bis neun beschriftet sind, bei denen aber durch ein Sichtfenster jeweils nur die aktuelle Ziffer sichtbar ist.
Videos
Im ersten Video wird auch auf das umfangreiche Lebenswerk Wilhelm Schickards eingegangen.
Die erste digitale mechanische Rechenmaschine
Die erste digitale mechanische Rechenmaschine wurde 1623 von Wilhelm Schickard erfunden. Im Film wird anhand eines Nachbaus dieser Maschine die Addition, Subtraktion und Multiplikation gezeigt. Außerdem wird kurz auf das sehr vielfältige Lebenswerk ihres Erfinders Wilhelm Schickard eingegangen.
Schickard Rechenmaschine versus Antikythera Mechanismus – Gemeinsamkeiten und Unterschiede
In diesem Video wird die älteste analoge Rechenmaschine mit der ältesten digitalen Maschine verglichen – der Antikythera Mechanismus versus die Schickard Rechenmaschine von 1623. Beide haben gemeinsam, dass sie rein manuell zu bedienen waren und für die Berechnungen Zahnräder nutzten.Was aber ist der Hauptunterschied? Es ist der Unterschied zwischen analog und digital. Dies wird anhand eines Rechenbeispiels verdeutlicht.
Addition und Subtraktion mit der Schickard-Rechenmaschine von 1623
In diesem Video werden Aufbau und Funktionsweise des Addierwerks der Schickard-Maschine gezeigt. Außerdem wird anhand eines Nachbaus in Aktion gezeigt, wie man mit der Maschine addieren und subtrahieren kann.
Multiplikation mit der Schickard-Rechenmaschine von 1623
und mit Napier'schen Rechenstäbchen
Anhand eines Nachbaus der 1623 von Wilhelm Schickard erfundenen Rechenmaschine wird die Multiplikation mit dieser Maschine gezeigt.
Der Aufbau des Multiplizierwerks wird erleutert. Da das Multiplizierwerk der Schickard'schen Maschine auf den Rechenstäbchen von John Napier basiert,
wird auch die Multiplikation mit diesen Stäbchen erläutert.
Division mit der Schickard-Rechenmaschine von 1623
Mit der 1623 von Wilhelm Schickard erfundenen Rechenmaschine konnten bereits alle vier Grundrechenarten berechnet werden. In diesem Video wird die Division gezeigt. Zunächst wird anhand eines einfachen Beispiels der Division zweier ganzer Zahlen die Vorgehensweise beim Dividieren erläutert. Danach wird gezeigt, dass es bereits mit dieser fast 400 Jahre alten Maschine möglich war, eine Gleitkommadivision durchzuführen.
Berechnung der Quadratwurzel 13 mit der Schickard-Rechenmaschine von 1623
In diesem Video wird am Beispiel der Wurzel 13 gezeigt, wie man mit der Schickard-Rechenmaschine Quadratwurzeln berechnen konnte.